Révisions algorithmique
Sauvegardes
Il est impératif de sauvegarder régulièrement le code en le collant dans un fichier texte (Notepad++) ou dans l'éditeur de pyzo.
Rappels - Boucles - Fonctions
- Ecrire un script qui calcule la somme des carrés des entiers de 1 à 1 million.
- Ecrire un script qui renvoie le premier entier n tel que \(\sum\limits_{i = 1}^n {i^2 \ge 10^6} \).
- Ecrire une fonction somme2(n) qui renvoie la somme des carrés des entiers de 1 à n.
A) Algorithmes de recherche
A.1 - Recherche d'un élément
Ecrire une fonction recherche(x, L) dont les paramètres sont un élément x et une liste L (supposée non vide). Cette fonction doit retourner un booléen (suivant que x est dans la liste ou non).
Tester cette fonction avec des listes variées (contennant des nombres et des chaînes... x étant en première position, en position quelconque ou en dernière position.)
A.2 - Recherche du plus grand élément d'une liste de nombres
Ecrire une fonction plusGrand(L) dont le paramètre est une liste L. Cette fonction doit retourner la plus grande valeur de L (supposée constituée uniquement de nombres).
Tester cette fonction avec des listes variées (vide, contennant des nombres et des chaînes... x étant en première position, en position quelconque ou en dernière position.)
B) Histogramme et tri (d'après concours)
B.1 - Histogramme d'un tableau d'entiers
Nous travaillons ici avec des listes qui ne contiennent que des chiffres (de 0 à 9).
Écrire la fonction hist(L) qui retourne un histogramme (sous la forme d’une liste) des chiffres présents dans la liste L.
Rappel : l’histogramme H est une liste telle que H[i] est le nombre d’occurrences (apparitions) de la valeur i dans la liste L.
Exemple : l'histogramme H de la liste L = [1,5,9,3,0,1,2,0,1,0,2,5,0,5,2,0] est [5, 3, 3, 1, 0, 3, 0, 0, 0, 1] car dans la liste L on trouve :
- 5 fois la valeur 0
- 3 fois la valeur 1
- 3 fois la valeur 2
- ...
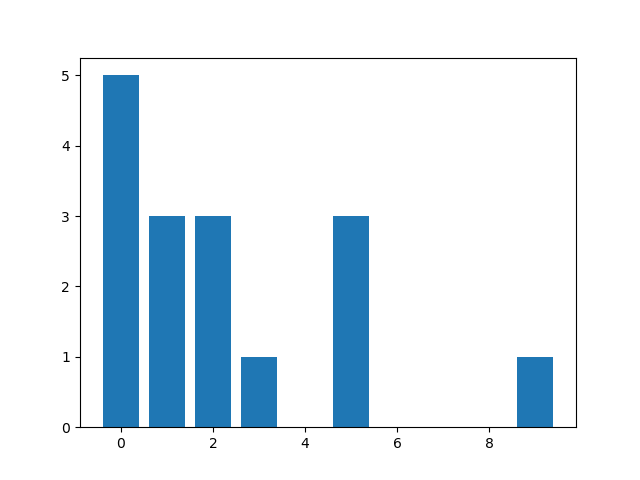
On représente un histogramme par un diagramme bâtons :
- abscisses = valeurs possibles
- ordonnées = nombre d’occurrences de chaque valeur
B.2 - Application au tri d'un tableau d'entiers
Utiliser la fonction hist pour écrire la fonction tri(L) qui trie la liste L en ordre croissant (la fonction construit une nouvelle liste qui doit être retournée).