Images en niveaux de gris - Contraste

Visuellement, pour une image en niveau de gris, le contraste est :
- nul pour une image uniformément grise ;
- maximum si chaque pixel est soit noir soit blanc.

Cette notion est donc liée à l'histogramme de luminosité, obtenu par exemple avec le logiciel GIMP (menu Couleurs / Informations / Histogramme), c'est à dire le nombre de pixels possèdant un niveau de gris donné :

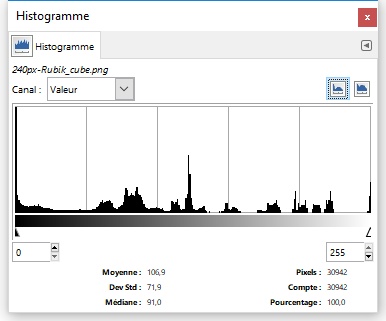
Histogramme = ensembles de couples (niveau de gris, nombre de pixels possédant ce niveau de gris) où le niveau de gris est un nombre 0 ≤ n ≤ 255 pour un codage sur 8 bits.

Le contraste C est défini par : $C = displaystyle\frac{I_{max}-I_{min}}{I_{max}+I_{min}}$.

Sur les quatre simulations ci-dessous (franges d'interférence), correspondant à quatre valeurs de contraste, en rouge la courbe de l'intensité I(x) est superposée à l'éclairement correspondant en niveau de gris :

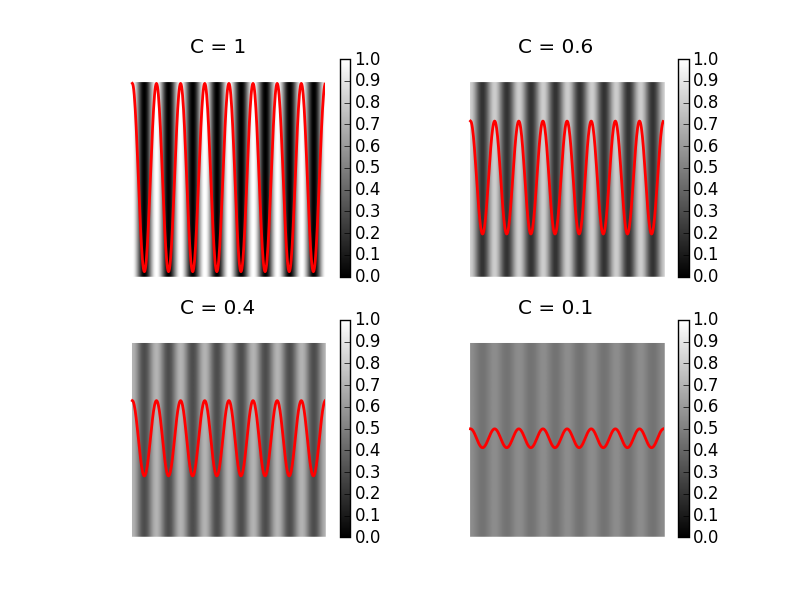
Davantage de détails : Contraste (Wikipédia).

On modifie le contraste d’une image (la courbe des tons) à l’aide d’une fonction de transformation (appliquée au niveau de gris de chaque pixel).
Dans le cas d’une image en niveaux de gris, cette fonction associe une nouvelle valeur (axe vertical) à la valeur initiale d’un pixel (axe horizontal) : ci-dessous, copies d'écrans du logiciel GIMP (menu Couleurs / Courbes...).

Ainsi, la fonction f(x) = x ne modifie pas le contraste initial (x et f(x) varient de 0 à 255 par exemple) : à une valeur de gris n dans l'image initiale, on fait correspondre la même valeur n dans l'image finale (ci-dessous).

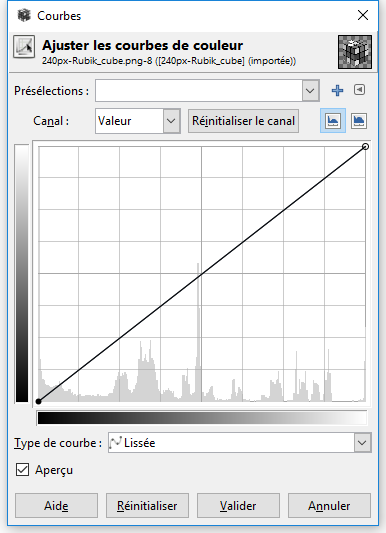
Toute fonction, autre que la fonction f(x) = x associera, à une valeur de gris n dans l'image initiale, une valeur différente dans l'image finale.
Ainsi, la fonction, en forme de "S" ci-dessous :
- associe à un pixel foncé (n "faible"), un pixel encore plus foncé (pente faible : f(x) < 1) ;
- associe à un pixel clair (n "grand"), un pixel encore plus clair pour la même raison ;
- varie très vite au voisinage des valeurs de gris moyennes (pente forte : f(x) > 1) donc on passe très vite des pixels foncés aux pixels clairs.
Conséquence : la fonction, en forme de "S" réduit la gamme de gris intermédiaires en renforçant les teintes foncées et les teintes claires, le contraste est donc augmenté.

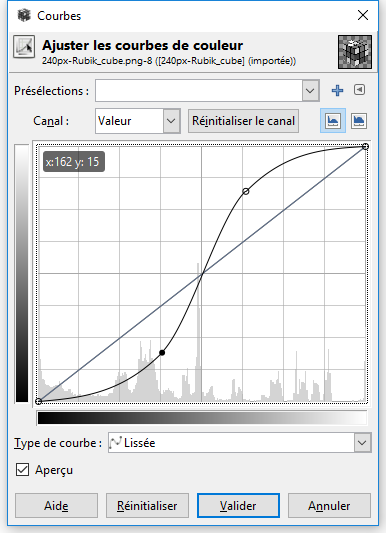
Pour une image en niveaux de gris, cette fonction de transformation f prend donc en entrée un entier 0 ≤ x ≤ 255 et renvoie un entier f(x) dans le même intervalle.

Contraste

La définition mathématique du contraste est à connaître (cf. chapitre interférences en physique). $$C = \frac{I_{max}-I_{min}}{I_{max}+I_{min}}$$

Sauvegardes

Il est impératif de sauvegarder régulièrement le code en le collant dans un fichier texte (Notepad++) ou dans l'éditeur de pyzo.

Remarque : dans cette page, les pixels des images en niveaux de gris sont des nombres (shape ne renvoie que 2 valeurs, le nombre de lignes et de colonnes).

Exercice 1 - Contraste

L'image utilisée est : 'http://gilles.django.group/static/images/Newton_Blake.png'
(image originale par William Blake — The William Blake Archive, Domaine public, Lien)

1.1 Augmenter le contraste de l'image.

Appliquer une fonction f(x) en forme de "S" à chaque pixel de l'image.
La fonction f(x) = 0.5+0.5*sin(pi*(x-0.5)) convient (éventuellement composée avec elle-même pour accentuer davantage le contraste).
Attention, cette fonction est une bijection sur l'intervalle [0,1] or les niveaux de gris sont compris entre 0 et 255 : on divisera donc chaque niveau de gris par 255 avant de lui appliquer la fonction f et on multipliera le résultat par 255 afin de ramener les valeurs dans l'intervalle [0, 255].

Exercice 2 - Histogramme

L'image utilisée est toujours : 'http://gilles.django.group/static/images/Newton_Blake.png'

2.1 Ecrire une fonction histogramme(Tab) permettant de tracer l'histogramme de luminosité du tableau Tab.

Cf. définition ci-dessus : valeurs de gris en abscisse (entiers de 0 à 255) et nombre de pixels pour chaque valeur de gris en ordonnée.

2.2 Comparer les histogrammes de l'image initiale et de l'image traitée pour augmenter le contraste.

Exercice 3 - Lumière

L'image utilisée est toujours : 'http://gilles.django.group/static/images/Newton_Blake.png'

Objectif : assombrir ou éclaircir l'image.

3.1 Ecrire une fonction fonce(Tab) appliquant la fonction $f(x) = x^2$ à chaque pixel.

Attention, 255² = 65 025 or pour une image en niveaux de gris codée sur 8 bits les valeurs vont de 0 à 255.
Il est donc nécessaire de créer une image codée sur 16 bits :
T = np.zeros((nombre_lignes, nombre_colonnes), dtype=np.uint16)

3.2 Ecrire une fonction clair(Tab) appliquant la fonction $f(x) = \displaystyle\sqrt(x)$ à chaque pixel.

3.3 Comparer les histogrammes de l'image initiale et de l'image éclaircie (l'image assombrie n'est pas directement comparable car elle est codée sur 16 bits).

❮ ❯