Convolution
La convolution d’image consiste à modifier la valeur d’un pixel en fonction des valeurs des pixels voisins.
La convolution utilise un tableau N(i,j) appelé
noyau de taille (2p+1)x(2p+1) où p est un entier strictement positif. Les effets obtenus dépendent du remplissage de ce tableau.
Ce noyau est visible et modifiable dans un logiciel tel que GIMP (menu Filtres / Génériques / Matrice de convolution...), ici noyau identité :
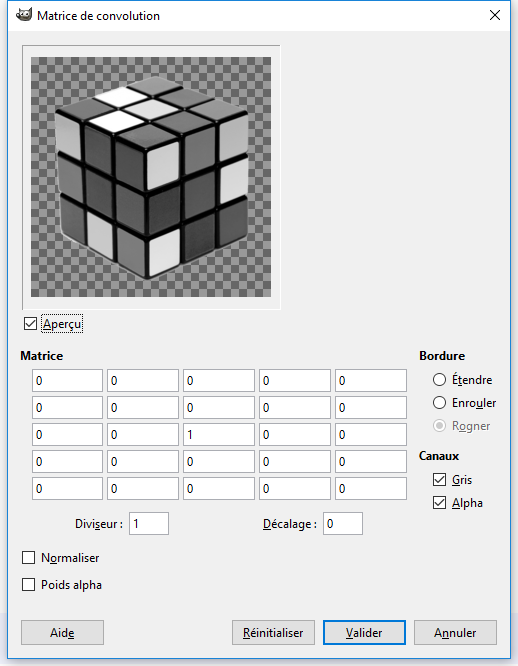
Le nouveau tableau-image \(T_{mod}\) est obtenu à partir du tableau-image T initial par : $$T_{mod}(i,j) = \sum\limits_{i_N = 0}^{2p} {\,\,\sum\limits_{j_N = 0}^{2p} {N(i_N, j_N)*T(i + i_N - p,j + j_N - p)}} $$ Ou bien : $$T_{mod}(i,j) = \sum\limits_{i_N = -p}^{p} {\,\,\sum\limits_{j_N = -p}^{p} {N(i_N, j_N)*T(i + i_N,j + j_N)}} $$
Exemple : noyau identité (l'image est inchangée avec ce noyau) :
$$N = \left( {\begin{array}{*{20}{c}} 0&0&0\\ 0&1&0\\ 0&0&0 \end{array}} \right)$$Remarques :
- Les pixels du bord de l'image ne peuvent pas être traités (ils n'ont pas de voisin dans au moins une direction), il faut donc décider d'une stratégie les concernant (les ignorer, dupliquer les pixels voisins, rogner l'image finale...).
- Après convolution, il peut être nécessaire d'appliquer une fonction pour que les valeurs des pixels restent comprises entre 0 et 255 (étape de normalisation).
Application au traitement d'images
Le traitement d'image possède d'innombrables applications : détection de contours afin de compter des objets ou de déterminer leurs points de contact, reconnaissance d'images par les moteurs de recherche, identification d'empreintes digitales, de visages...
Autres noyaux
Exemples de noyaux :
| Effet | Noyau |
|---|---|
| Netteté ou accentuation | $$ N = \left( {\begin{array}{*{20}{c}} 0&{ - 1}&0\\ { - 1}&5&{ - 1}\\ 0&{ - 1}&0 \end{array}} \right)$$ |
| Détection des bords | $$ N = \left( {\begin{array}{*{20}{c}} 0&1&0\\ 1&{ - 4}&1\\ 0&1&0 \end{array}} \right)$$ |
Autres noyaux sur le site Matrice de convolution (gimp.org).
Sauvegardes
Il est impératif de sauvegarder régulièrement le code en le collant dans un fichier texte (Notepad++) ou dans l'éditeur de pyzo.
Remarque : dans cette page, les pixels des images en niveaux de gris sont des nombres (shape ne renvoie que 2 valeurs, le nombre de lignes et de colonnes).
Exercice 5 - Convolution
L'image utilisée est : 'http://gilles.django.group/static/images/240px-Rubik_cubeNB.bmp'
5.1 On donne la fonction convolution(m, N) qui résulte directement de la formule fournie dans le paragraphe "Convolution" et la fonction normalise(T).
A titre d'entraînement ou de révision, s'entraîner à écrire ces fonctions.
5.2 On donne le noyau identité (observer la syntaxe).
5.3 Tester le noyau identité sur le tableau-image : l'image doit être inchangée si le script est correct (compléter le code).
5.4 Comment définir le noyau réalisant une moyenne sur les pixels immédiatement voisins ?
5.5 Tester les noyaux proposés dans cette page et observer leurs effets.