LateX - Formules mathématiques
Le langage LaTeX est utilisé pour écrire des formules mathématiques. Toutes les formules de ce site sont écrites dans ce langage.
Un clic droit sur une formule dans ces pages permet de voir la syntaxe de la formule : choisir "Show Math As" puis "TeX Commands".
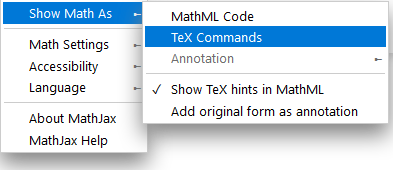
Exemple : \(E_c = \frac{1}{2} m v^2\) (essayer le clic droit pour voir le code).
Sur le site du cahier de textes, les équations sonté délimitées par : \( et \).
Quelques liens :
Tuteurs ENS
Wikibooks LaTeX
Construction de formules
L'ajout de \displaystyle modifie la taille de la formule (fractions, intégrales, limites, sommes, produits).
Les bornes sont placées à côté des symboles par _{début}^{fin} et au-dessous/au-dessus des symboles par \limits_{début}^{fin}.
Les accolades peuvent être omises lorsque elles ne contiennent qu'un seul caractère. Par exemple : \vec u et \vec {u} donnent \(\vec u\).
| Opérateur | Syntaxe | Exemple code/rendu |
|
|---|---|---|---|
| Exposant Indice |
^{...}_{...} |
e^{-5}H_{max} |
\(e^{-5}\) \(H_{max}\) |
| Fraction | \frac{...}{...} |
\displaystyle\frac{a}{b}\frac{a}{b} |
\(\displaystyle\frac{a}{b}\) \(\frac{a}{b}\) |
| Racine | \sqrt{...} |
\sqrt{2} |
\(\sqrt{2}\) |
| Dérivées | \dot {...} |
\dot x |
\(\dot x\) \(\ddot x\) |
| Intégrale simple | \int_{debut}^{fin}... |
\displaystyle\int_{0}^{1}f(x)dx\displaystyle\int \limits_{0}^{1} f(x)dx\int_{0}^{1}f(x)dx |
\(\displaystyle\int_{0}^{1}f(x)dx\) \(\displaystyle\int \limits_{0}^{1} f(x)dx\) \(\int_{0}^{1}f(x)dx\) |
| Intégrale double | \iint_{debut}^{fin}... |
\(\displaystyle\iint_{0}^{1}f(x)dx\) | |
| Intégrale triple | \iiint_{debut}^{fin}... |
\(\displaystyle\iiint_{0}^{1}f(x)dx\) | |
| Intégrale chemin fermé | \oint_{debut}^{fin}... |
\(\displaystyle\oint_{0}^{1}f(x)dx\) | |
| Intégrale surface fermée | N'existe pas |
\mathop{{\displaystyle\int\!\!\!\!\!\int}\mkern-20mu \bigcirc}{\large\bigcirc}\kern-1.55em\displaystyle\iint\) |
\(\mathop{{\displaystyle\int\!\!\!\!\!\int}\mkern-20mu \bigcirc} \vec E \cdot d\vec S\) \({\large\bigcirc}\kern-1.55em\displaystyle\iint {\vec E. d \vec S}\) |
| Limite | \lim_{... \to ... }... |
\displaystyle\lim_{x \to 0 }f(x)\lim_{x \to 0 }f(x) |
\(\displaystyle\lim_{x \to 0 }f(x)\) \(\lim_{x \to 0 }f(x)\) |
| Somme Produit |
\sum_{debut}^{fin}...\prod_{debut}^{fin}... |
\sum_{n=0}^{10} n\prod_{n=0}^{10} n |
\(\sum_{n=0}^{10} n\) \(\prod_{n=0}^{10} n\) |
| Vecteurs | \vec{...}\overrightarrow{...} |
\vec{v}\overrightarrow{AB} |
\(\vec{v}\) \(\overrightarrow{AB}\) |
| Complexes | \underline{...} |
\underline{z} |
\(\underline{z}\) |
| Valeurs algébriques | \overline{...} |
\overline{AB} |
\(\overline{AB}\) |
| Structures complexes | \mathop {...} \limits^{...} |
\mathop {=} \limits^{def}\mathop {\longrightarrow} \limits_{x \to 0}^{y=a} |
\(\mathop {=} \limits^{def}\) \(\mathop {\longrightarrow} \limits_{x \to 0}^{y=a}\) |
| Autres | \underbrace{...}_{...} |
\underbrace{1+2+\cdots+10}_{10 \textrm{ fois}} |
\(\underbrace{1+2+\cdots+10}_{10 \textrm{ nombres}}\) |
Symboles
| Symbole | Syntaxe | Exemple code/rendu |
|
|---|---|---|---|
| Dérivée partielle | \partial |
|
\(\partial\) |
| Prime | \prime |
f^{\prime} |
\(f^{\prime}\) |
| ∞ | \infty |
|
\(\infty\) |
| ℏ | \hbar |
|
\(\hbar\) |
| ℓ | \ell |
|
\(\ell\) |
| Nabla | \nabla |
|
\(\nabla\) |
| ⊥ | \bot |
|
\(\bot\) |
| ∀ ∃ |
\forall\exists |
|
\(\forall\) \(\exists\) |
| ℜ ℑ |
\Re\Im |
\(\Re\) \(\Im\) |
|
| ∅ | \emptyset |
|
\(\emptyset\) |
Opérateurs binaires
| Opérateur | Syntaxe | Rendu |
|---|---|---|
| Multiplication × | \times |
\(\times\) |
| Produit scalaire ˙ | \cdot |
\(\cdot\) |
| Produit vectoriel ∧ | \wedge |
\(\wedge\) |
| ± | \pm |
\(\pm\) |
Opérateurs de relation
| Opérateur | Syntaxe | Rendu |
|---|---|---|
| ≤ ≥ ⪡ ⪢ |
\leq\geq\ll\gg |
\(\leq\) \(\geq\) \(\ll\) \(\gg\) |
| ∼ ≃ ≈ ≠ |
\sim\simeq\approx\neq |
\(\sim\) \(\simeq\) \(\approx\) \(\neq\) |
| ≡ ∝ |
\equiv\propto |
\(\equiv\) \(\propto\) |
Fonctions
Faire précéder le nom de la fonction de \. Exemples : \sin, \log...
Fonctions non usuelles : \mathrm{...}. Exemple : \(\mathrm{f}(x)\).
Flèches
Majuscule pour passer de la flèche simple à la flèche double. Ajouter long ou long devant le nom de la flèche pour l'allonger.
| Flèche | Syntaxe | Rendu |
|---|---|---|
| → ⇒ ⟶ ⟹ |
\rightarrow\Rightarrow\longrightarrow\Longrightarrow |
\(\rightarrow\) \(\Rightarrow\) \(\longrightarrow\) \(\Longrightarrow\) |
| ← ⇐ ⟵ ⟸ |
\leftarrow\Leftarrow\longleftarrow\Longleftrrow |
\(\leftarrow\) \(\Leftarrow\) \(\longleftarrow\) \(\Longleftarrow\) |
| ↔ ⇔ ⟷ ⇔ |
\leftrightarrow\Leftrightarrow\longleftrightarrow\LongLeftrightarrow |
\(\leftrightarrow\) \(\Leftrightarrow\) \(\longleftrightarrow\) \(\Longleftrightarrow\) |
Polices - Lettres grecques
Ensembles
\mathbb{C} donne \(\mathbb{C}\). On obtient de façon analogue : \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\), \(\mathbb{R}\).
Ecriture manuscrite
\mathcal(A) : \(\mathcal(A)\), \(\mathcal(a)\),...
Texte non mathématique
\textrm{...}} ou \text{...} ou \mbox{...} : \(\textrm{Abcd efg}\), , \(\text{Abcd efg}\), \(\mbox{Abcd efg}\)
Rq : \mathrm{...} supprime les espaces : \(\mathrm{Abcd efg}\) (utilisé pour les fonctions).
Lettres grecques
Faire précéder le nom de la lettre (minuscule ou majuscule) de \ (ou éventuellement de \var pour certaines lettres, cf. exemples).
| Lettre | Syntaxe | Rendu |
|---|---|---|
| α β γ δ Γ Δ |
\alpha \beta \gamma \delta\Gamma \Delta |
\(\alpha\) \(\beta\) \(\gamma\) \(\alpha\) \(\Gamma\) \(\Delta\) |
| ϵ ϕ |
\varepsilon\varphi |
\(\varepsilon\) \(\varphi\) |
Délimiteurs
Faire précéder le nom du délimiteur (brack, brace, floor, ( ou )) de \l (pour left) ou de \r
(pour right).
Les délimiteurs s'adaptent à la taille du contenu.
| Délimiteur | Syntaxe | Exemple code/rendu |
|
|---|---|---|---|
| [ ] | \lbrack \rbrack |
|
\(\lbrack\) \(\rbrack\) |
| { } | \lbrace \rbrace |
|
\(\lbrace\) \(\rbrace\) |
| ⌊ ⌋ | \lfloor \rfloor |
|
\(\lfloor\) \(\rfloor\) |
| ( ) | \left ( ... \right ) |
\left ( \displaystyle\frac a b \right )( \displaystyle\frac a b ) |
\(\left ( \displaystyle\frac a b \right )\) \( ( \displaystyle\frac a b ) \) |
Espaces
| Espace | Syntaxe | Exemple code/rendu |
|
|---|---|---|---|
| Fin | \, |
a \, bab |
\(a \, b\) \(a b\) |
| Moyen | \; |
a \; bab |
\(a \; b\) \(a b\) |
| Large | \: |
a \: bab |
\(a \: b\) \(a b\) |
| Normal (intermot) | \ |
a \ bab |
\(a \ b\) \(a b\) |
| Cadratin | \quad |
a \quad bab |
\(a \quad b\) \(a b\) |
| Double cadratin | \qquad |
a \qquad bab |
\(a \qquad b\) \(a b\) |
| Espace négatif | \! |
Cf. intégrale double fermée | |
Pointillés
| Pointillés | Syntaxe | Exemple code/rendu |
|
|---|---|---|---|
| Bas | \dots |
1 + \dots + 10 |
\(1 + \dots + 10\) |
| Centrés | \cdots |
1 + \cdots + 10 |
\(1 + \cdots + 10\) |
Tableaux - Matrices
Les délimiteurs ouvrants sont de la forme \left (, \left |... et \right (, \right |...
En cas de délimiteur unique à gauche, terminer par \right . ).
Le tableau débute par \begin{array}{alignement} et se termine par \end{array}.
Saut de ligne : \\.
Saut de colonne : &.
"Alignement" est de la forme x x ... x (autant de fois que de colonnes) où x est parmi : l, c, r, | (alignements à gauche, droite, centré, trait vertical entre deux colonnes).
| Opérateur | Syntaxe | Exemple |
|---|---|---|
| Coordonnées |
\left| \begin{array}{l}Variante : \left| \begin{align*}
|
\(\left| \begin{array}{l}
x \\
y \\
z \\
\end{array} \right.\) \(\left| \begin{align*} &x \\ &y \\ &z \\ \end{align*} \right.\) |
| Matrice |
\left(
|
\(\left( \begin{array}{ c c } 1 & 2 \\ 3 & 4 \end{array} \right)\) |
| Tableau | \begin{array}{l|cr} |
\(\begin{array}{l|cr}1 & 2 & 3\\ \hline 4 & 5 & 6\\ 7 & 8 & 9\\\end{array}\) |
Equations alignées
\begin{eqnarray} ... \end{eqnarray} avec sauts de ligne \\ et sauts de colonne &.
Ou bien \begin{equation}\begin{split} ... \end{split}\end{equation} (cf. exemples ci-dessous).
Compléments.
| Exemple | Rendu |
|---|---|
\begin{eqnarray}
|
\(\begin{eqnarray} 5x-6&=&-1\\ 5x&=&5\\ x&=&1 \end{eqnarray}\) |
\begin{equation}
|
\(\begin{equation} \begin{split} x & = -7a -1 + 9a \\ & = 2a - 1 \end{split} \end{equation}\) |