Sensation de chaud et de froid - Effusivité thermique

Lorsqu’on pose la main sur une table en bois et sur une table en métal, toutes deux à la température ambiante, la table en métal paraît plus « froide » que la table en bois.
On se propose d’expliquer cette sensation d’une part à l’aide d’un modèle très simple d’autre part à l’aide de solutions de l’équation de diffusion.
On note \(\lambda_1\), \(\lambda_2\) les conductivités thermiques, \(D_1\), \(D_2\) les diffusivités thermiques et \(T_1(x,t)\), \(T_2(x,t)\) les températures respectivement dans la main et
dans la table.
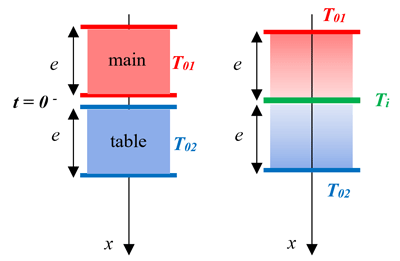
Les conditions initiales, à l’instant t = 0 où la main entre en contact avec la table sont :
- \(T(x < 0, t=0) = T_{01} =\) 37 °C (main)
- \(T(x > 0, t=0) = T_{02} =\) 17 °C (table)
1. Préliminaires
Rappeler les unités de λ et D.
2. Contact prolongé - Sensation de froid (difficulté *)
Modélisation :
- évolution stationnaire ;
- main et table d'épaisseurs voisines notée e (de l'ordre du cm).
2.a Etablir les expressions de \(T_1(x,t)\) et \(T_2(x,t)\) en fonction de \(x, \, e, \, T_{01}, \, T_{02}\) et \(T_i\) la température à l'interface (inconnue à ce stade).
2.b On suppose que la température est continue en x = 0 à partir de t < 0. Justifier la continuité de la densité de flux thermique \(j_Q(x, t)\) en x = 0 en appliquant le 1er principe à un élément de surface dS (d’épaisseur nulle) de l’interface.
2.c En déduire \(T_i\).
2.d A.N. \( \lambda_\textrm{main} = 10 \,\, \textrm{W} \, \textrm{m}^{-1} \, \textrm{K}^{-1} \), \( \lambda_\textrm{bois} = 1 \,\, \textrm{W} \, \textrm{m}^{-1} \, \textrm{K}^{-1} \),
\( \lambda_\textrm{acier} = 100 \,\, \textrm{W} \, \textrm{m}^{-1} \, \textrm{K}^{-1} \).
Commenter.
2.e e. Montrer que l’expression de \(T_i\) peut facilement être déterminée à l’aide d’une analogie électrique.
3. Contact bref - Notion d'effusivité (difficulté ** facultatif)
Modélisation :
- évolution non stationnaire (étude dynamique);
- la main est assimilée au demi-espace x < 0 (température \(T_1(x,t)\)) et la table au demi-espace x > 0 (température \(T_2(x,t)\)).
3.a On montre que les solutions de l'équation de la chaleur sont de la forme :
\( T_1(x,t) = \alpha _1 + \beta _1\displaystyle\int\limits_0^{u_1} e^{-z^2}\textrm{d}z \) où \( u_1 = \displaystyle\frac{x}{2\sqrt{D_1 t}} \)
\( T_2(x,t) = \alpha _2 + \beta _2\displaystyle\int\limits_0^{u_2} e^{-z^2}\textrm{d}z \) où \( u_2 = \displaystyle\frac{x}{2\sqrt{D_2 t}} \)
On rappelle que \( \displaystyle\frac{\partial }{\partial x}\left( \int\limits_0^{u(x,t)} g(z)\textrm{d}z \right) = g\left( u(x,t) \right) \left( \frac{\partial u}{\partial x} \right)_t \)
(dérivée composée).
Déterminer \(\alpha_1\), \(\beta_1\), \(\alpha_2\) et \(\beta_2\). On posera \( I = \displaystyle\int\limits_0^\infty e^{-z^2}\textrm{d}z \).
3.b En déduire que la température de l’interface se met sous la forme \( T_i = \displaystyle\frac{E_1 T_{01} + E_2 T_{02}}{E_1 + E_2} \) où l’effusivité E est une caractéristique du milieu qu’on exprimera en fonction de D et λ.
3.c A.N. : \(E_\textrm{main} = 10^3\) usi, \(E_\textrm{bois} = 10\) usi, \(E_\textrm{acier} = 10^4\) usi. Conclure.
3.d En réalité, la main et la table ont une épaisseur finie e ≈ 1 cm. Montrer que le modèle des demi-espaces infinis reste valable si le contact est suffisamment bref et estimer la durée maximum de ce contact.
1. Question de cours
Pour retrouver les unités ou les dimensions d'une grandeur, il faut utiliser une relation (aussi simple que possible) dans laquelle elle est impliquée.
2.a Faire un schéma annoté (main, table, épaisseur, axe du repère, températures).
On considère que la température du dessus de la main et du dessous de la table ne sont pas affectées par le contact.
2.b Question de cours
2.c Loi de Fourier avec les expressions de 2.a et continuité démontrée en 2.b
2.d A.N. en vue de valider ou non le modèle.
2.e Utilisation de la résistance thermique
3.a Conditions aux limites et conditions initiales
3.b Elimination de I
3.c A.N. en vue de valider ou non le modèle.
3.d Critique du modèle (1/2 espaces infinis)