Transfert d'orbites
(d'après Mines-Telecom)La Terre est supposée à symétrie sphérique, de centre C, de rayon \(R_T\) et de masse \(M_T\).
On donne : \(R_T = 6400 \) km, \(M_T = 6,0 \cdot 10^{24}\) kg et la constante universelle de gravitation \(G = 6,674 \cdot 10^{-11} \, \si N \si [2]m \si [-2]{kg}\)
- Un satellite géostationnaire décrit une trajectoire située dans le plan équatorial.
Définir ce qu’est un satellite géostationnaire, déterminer son altitude ainsi que sa vitesse. -
Le satellite est au départ sur une orbite circulaire de rayon \(r_1 = 7500 \si{km}\) autour de la Terre, on souhaite le faire passer de manière définitive sur l’orbite géostationnaire de rayon \(r_2\)
déterminée précédemment. Un moteur auxiliaire permet de modifier la vitesse du satellite aux points P et A. Le satellite parcourt alors une demi-ellipse, dite de transfert, de périgée P et d’apogée A.
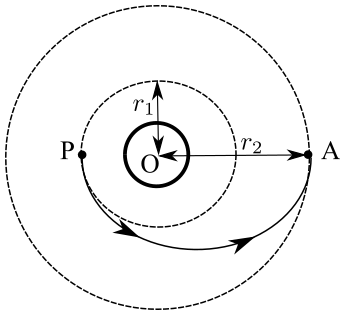
- Montrer que sur la trajectoire elliptique, le produit \(C = r^2\dot\theta\) est une constante.
- Déterminer l’expression de l’énergie mécanique pour le satellite sur son orbite elliptique.
On pourra chercher à exprimer l'énergie mécanique en fonction de C et de \(\dot r\). Que peut-on dire des vitesses radiales A et en P, \(\dot r_A\) et \(\dot r_P\) ? En déduire une équation du second degré en r dont ne calculera que la somme des racines. - Déterminer la variation de vitesse \(\Delta v_1\) au point P pour faire passer le satellite sur l’orbite elliptique.
- En déduire la vitesse du satellite arrivant en A encore sur l’orbite elliptique.
Prérequis :
- Expression de la force de gravitation de Newton et de l'énergie potentielle associée.
- Théorème du moment cinétique en un point (ou par rapport à un axe) fixe dans le référentiel d'étude.
- Expression de l'énergie sur une orbite elliptique identique à celle de l'orbite circulaire à condition de remplacer le diamètre par le grand axe.
- Somme des racines de l'équation \(ax^2+bx+c=0\) : \(-\dfrac{b}{a}\)
Savoir-faire :
- Problèmes liés aux satellites : PFD appliqué au satellite dans le référentiel géocentrique supposé galiléen (en coordonnées polaires dans le plan de la trajectoire).
- Force centrale \(\Rightarrow\) trajectoire plane (vecteurs position et vitesse orthogonaux à tout instant au vecteur moment cinétique constant).
- Constante des aires obtenue via le TMC.
- Satellite géostationnaire
- Transfert
- Constante des aires
- Energie mécanique
- Variation de vitesse
- Vitesse en A