Pendule à extrémité supérieure mobile
(d'après CCINP)Un pendule simple constitué d'un fil de longueur \(\ell\) de masse nulle et d'une masse ponctuelle \(m\) est suspendu en un point A.
Ce point A effectue dans le référentiel terrestre galiléen des oscillations le long de l'axe horizontal (Ox), autour d’un point fixe O (non représenté) telles que
\( \overrightarrow{OA} = a \sin(pt) \, \vec u_x \).
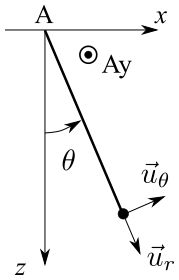 Le pendule oscille dans un plan vertical et on appelle \(\theta\) l’angle formé par le fil avec la verticale passant par A.
Le pendule oscille dans un plan vertical et on appelle \(\theta\) l’angle formé par le fil avec la verticale passant par A.
On considère deux référentiels \(R(Oxyz)\) et \(R^{\prime}(Axyz)\).
- Que peut-on dire du référentiel \(R^{\prime}\) ?
- Faire le bilan des forces s’exerçant sur M et les exprimer en coordonnées polaires.
- Appliquer le théorème du moment cinétique par rapport au point A.
En déduire l’équation différentielle vérifiée par \(\theta\). - La résoudre dans l’approximation des petits angles pour \(\theta\) sachant que \(\theta(0)=0\) et \(\dot\theta(0)=0\).
Prérequis :
- Expression de la force d'inertie d'entraînement dans un référentiel non galiléen en translation par rapport à un référentiel galiléen.
- Théorème du moment cinétique en un point (ou par rapport à un axe) fixe dans le référentiel d'étude.
Savoir-faire :
- Résolution d'une équation différentielle linéaire à coefficients constants dans le cas d'une excitation sinusoïdale (régime forcé).
- Choix du référentiel
- Forces
- TMC
- Intégration