Glissade sur un igloo
(d'après CCINP)Un enfant de masse \(m\) assimilé à un point matériel M glisse sans frottement sur un igloo sphérique de rayon \(R\).
L'enfant commence à glisser à \(t=0\) à partir du sommet sans vitesse initiale.
Il est repéré par l'angle \(\theta(t)\) avec \(\theta(0)=0\) dans le plan de la trajectoire (plan de symétrie de l'igloo).
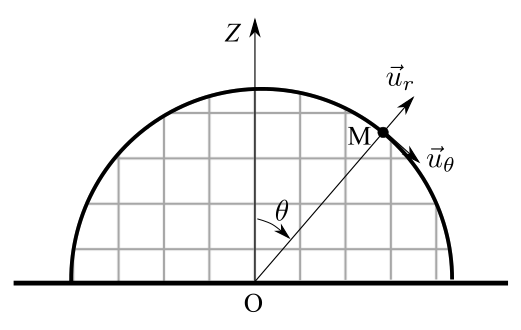
- Effectuer le bilan des forces sur l'enfant.
- Ecrire le principe fondamental de la dynamique pour l'enfant, en projection sur la base polaire.
- Ces deux équations sont-elles facilement exploitables ? Justifier.
- Intégrer l'équation orthoradiale après avoir multiplié les deux membres par \(\dot\theta\).
Vérifier que cette intégration peut être évitée en utilisant un théorème énergétique entre l'instant initial et l'instant \(t\).
En déduire une relation entre \(\dot{\theta}(t)\) et \(\theta(t)\). - Donner l'expression de la réaction de l'igloo sur l'enfant en fonction de sa position \(\theta\).
- L'enfant décolle-t-il ? Si oui pour quel angle ?
Prérequis :
- Formule de l'accélération en coordonnées polaires pour un mouvement circulaire.
- Propriétés de l'action de contact dans le cas de frottements négligés (lois de Coulomb du frottement solide).
Savoir-faire :
- Utilisation d'un théorème énergétique (intégrale première du mouvement) pour éviter une intégration non triviale.
- Condition de contact (liaison unilatérale).
- Bilan des forces sur l'enfant
- PFD pour l'enfant en polaires
- Analyse des équations
- Intégration
- Réaction de l'igloo sur l'enfant
- Décollage