Bille dans un tube tournant

(d'après Mines-Ponts)

Un tube creux tourne autour de l’axe vertical Oz avec une vitesse angulaire constante \(\omega\). Le tube est incliné d’un angle constant \(\theta\) par rapport à l’axe.
Un objet assimilé à un point matériel M de masse m peut glisser sans frottements dans ce tube.
On pose \(\vecteur{OM} = \vec r\).
A \(t=0\) , la vitesse du point, par rapport au tube, est nulle et \(r = r_0\) .

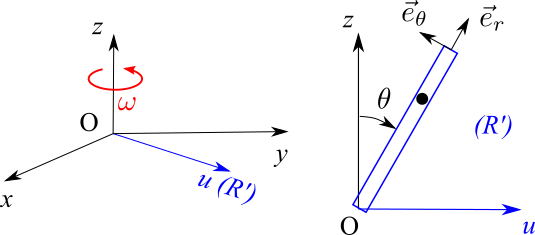
Préciser les forces s’exerçant sur la masse.
Déterminer l’équation différentielle vérifiée par \(r(t)\).
Combien de temps la masse met-elle à sortir du tube de longueur ℓ ?

Prérequis :

Expression de la force d'inertie d'entraînement dans un référentiel en rotation par rapport à un référentiel galiléen.

Savoir-faire :

Savoir ne pas calculer des forces dont l'expression n'est pas utile pour la détermination de l'équation du mouvement.

Forces

Dans le référentiel du tube (non galiléen car en rotation dans le référentiel terrestre), la bille est soumise à son poids, aux actions de guidage par les parois du tube ("réaction") orthogonales au tube car on néglige les frottements, à la force d'inertie d'entraînement et à la force d'inertie de Coriolis.
Equation du mouvement

L'équation du mouvement est obtenue en projetant la seconde loi de Newton sur \(\vec e_r\). Il est donc inutile d'exprimer la force de Coriolis qui est orthogonale au plan de la figure.
La force d'inertie d'entraînement est "axifuge" donc dirigée dans le sens du vecteur \(\vec u\) du schéma. Le point coïncident décrit un cercle centré sur l'axe Oz de rayon \(r\sin\theta\) à la vitesse angulaire \(\omega\) ⇒ \(\vec f_{ie}=m r\sin\theta \omega^2 \, \vec u\).
Après projection, on obtient : \(\ddot r - \omega^2\sin^2\theta \,\,r = - g\cos\theta\) (Attention, cette équation n'est pas celle d'un oscillateur !).
Temps de sortie

Pour déterminer le temps de sortie, il faut résoudre l'équation différentielle afin de déterminer \(r(t)\).
Le temps de sortie est alors obtenu en écrivant \( r(t_S) = \ell \).
Remarque : il existe une position d'équilibre (instable, puisque l'équation ne décrit pas des oscillations) pour laquelle les actions du poids et la force d'inertie d'entraînement sur la bille se compensent (i.e. leurs projections sur le tube).
Cette position d'équilibre est \(r_{eq} = \displaystyle\frac{g\cos\theta}{\omega^2\sin^2\theta} \).
On obtient finalement : \(r(t) = (r_0-r_{eq})\cosh(\omega\sin\theta t)+r_{eq} \).
On en déduit alors le temps de sortie à condition que \(r_0 > r_{eq}\) (sinon la bille chute au fond du tube).