Prérequis :

• Théorème d'Ampère.

Savoir-faire :

• Symétries et invariances

1. Symétries et invariances
Solution

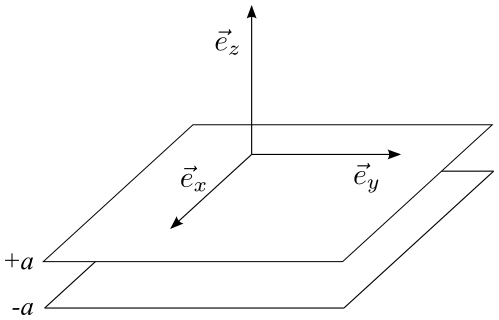
Soit un point M quelconque (donc hors du plan médiateur (Ox,Oy)).
Le plan parallèle à (Ox,Oz) passant par M est un plan de symétrie pour la distribution de courants donc \(\vec B(M) // \vec e_y\).
Les invariances par translation selon x et y permettent d'écrire \(\vec B(M) = B_y(z) \vec e_y\).
Remarques :
- Pour z > a, \(B_y(z) \lt 0\).
- Le plan médiateur (Ox,Oz) est un plan de symétrie pour la distribution
    ⇒ \(\vec B =\vec 0\) (1) en tout point de ce plan compte tenu des symétries précédentes ;
    ⇒ \(B_y(-z) = -B_y(z)\) (2).




2. Champ magnétique
Solution

Les lignes de champs sont donc des droites parallèles à (Oy). On choisit donc un contour d'Ampère (Γ) rectangulaire dont les côtés sont soit parallèles aux lignes de champ soit orthogonaux (contour dans un plan parallèle à (Oy,Oz)).
Deux choix possibles :
- contour (Γ) symétrique par rapport au plan médiateur ⇒ il faudra utiliser (2) ;
- l'un des côtés du contour (Γ) est sur (Oy) ⇒ il faudra utiliser (1).
Par ailleurs, deux cas sont à prévoir : cadre entièrement dans la distribution ou non (i.e. M à l'intérieur ou à l'extérieur de la distribution).
Indispensable : faire 2 schémas (un dans chaque cas) avec le vecteur champ et le vecteur déplacement élémentaire en plusieurs points du contour.
On trouve :
\(\begin{eqnarray} a \leq z & \ \ \ & \vec B(z)=-\mu_0 j_0 a \ \vec e_y\\ -a \leq z \leq a & \ \ \ & \vec B(z)=-\mu_0 j_0 z \ \vec e_y\\ z \leq -a & \ \ \ & \vec B(z)=\mu_0 j_0 a \ \vec e_y \end{eqnarray}\)